Método da seções
Quando precisamos encontrar a força em apenas alguns
membros de uma treliça, podemos analisar a treliça usando o método das seções.
Este método se baseia no princípio de que se uma treliça está em equilíbrio,
então qualquer segmento dela também está em equilíbrio.
Portanto, o método das seções também pode ser usado
para “cortar” ou seccionar os membros de uma treliça inteira. Como apenas três
equações de equilíbrio independentes podem ser aplicadas ao diagrama de corpo
livre de qualquer segmento (ΣFx = 0, ΣFy = 0, ΣMO = 0), então, tentaríamos
escolher uma seção que passe por não
mais que três membros em que
as forças são desconhecidas.
Seguiremos os seguintes passos para realizarmos os cálculos:
- Encontrar os ângulos;
- Encontrar as reações de apoio;
- Fazer um corte que divida o elemento desejado e mais dois outros no máximo;
- Representar "nós virtuais";
- Aplicar as reações de equilíbrio.
Exercício Resolvido
Determinar os esforços nas barras DF; EF e EG da
treliça abaixo, indicando se as barras estão sobre tração ou compressão.
Veja que fizemos o corte das barras onde queremos calcular as seções e que "cortamos" três barras.
- Calculando os ângulos.
2. Calculando as reações de apoio.
3. Fazendo o corte dos elementos.
Quando é realizado o corte, representamos as forças sempre "saindo" dos nós, como foi feito pelo método dos nós. Fizemos o corte e "olhamos" pelo lado direito da treliça, a escolha do lado fica a critério. O nó virtual ou imaginário seria o ponto E. Ele servirá como referencia para calcularmos o momento e eliminar as barras que chegam nele.
4. Aplicando as reações de equilíbrio.
Como foi dito, cancelamos as barras que chegam no nó virtual, restando apenas uma barras para ser calculada, que é a FDF. O cálculo do momento é feito normalmente. O FDF está a 0,8m do ponto é (que corresponde a altura), e as demais forças estão a distancia de 1m (força concentrada) e 2 m (VI).
Para calcularmos a força FEF, realizamos o somatório de forças verticais, pois assim teremos somente uma incógnita, não precisando assim realizar muitos cálculos. Iremos utilizar todas as forças que estão a direita do corte: a força FEF, força concentrada e a força VI. Utilizamos o seno pois como foi dito no post anterior, quando decompomos a força na vertical ela fica "sem" o ângulo.
A última força que o exercício pede é a FEG. Vamos utilizar o somatório de forças horizontais para realizar o cálculo. As forças que tem na horizontal é a FDF que já foi encontrada, a FDF que tivemos que decompor )desta fez utilizamos o cosseno, pois na horizontal está "com" o ângulo) e a FEG que é a força que queremos.
*Em relação ao sinal do FDF, ele é negativo pois está em sentido contrário ao da convenção. Entre parenteses ele está negativo pois quando foi feito o cálculo encontramos ele como compressão e não fizemos nenhuma correção no desenho, então carregamos do sinal.
Bom, mais um exercício resolvido, esperemos ter descomplicado um pouco. O blog está bem amador ainda, mas o conteúdo foi feito com muito carinho. Sua opinião é muito importante para nós. Deixe sua dúvida, críticas e elogios no comentário. Compartilhe com quem precisa.
Muito Obrigado à todos.







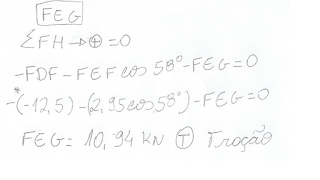
Nenhum comentário:
Postar um comentário